• Schémas TVD
• Analyse Multi-résolution
• Compression Artificielle (ACM)

Problème à surface libre.

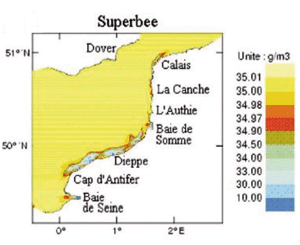Application de l'ACM à la simulation de la bande de dessalure dans la Manche Orientale.

Les schémas developpés sont TVD (Total Variation Diminishing). Pour certains, ils sont sym´etriques d’ordre deux, incorporant les idées clés des méthodes developpées pour les équations d’Euler compressibles. Comme les sauts hydrauliques se propagent à une vitesse différente de celle de la matière, ils induisent une augmentation d’entropie. Pour que la méthode numérique rende compte de ce phénomène, une dissipation d'énergie cinétique en énergie interne est induite au moyen d’un processus de diffusion de quantité de mouvement dans les zones où les variations de vitesse sont importantes. Pour renforcer le caractère “High Resolution” de la méthode, nous proposons un choix judicieux de flux numérique et des fonctions limiteur de flux pour le contrôle des zones de chocs et de discontinuités de contact. Nous avons établit une “Strong Conservationlaw Form” pour les équations de Saint-Venant (SWE). Ensuite, nous avons étendu le schéma TVD de Harten-Yee (via l’approche de modification de flux) au SWE, écrit dans un système de coordonnées généralisées.

La Multi-résolution est une méthode numérique permettant de représenter, au moyen de coefficients d'echelle locaux, des données issues d'une discrétisation de type TVD, ENO ou bien MUSCL. La multi-résolution est fondamentalement une méthode de compression de données associée à une analyse de régularité de la solution mathématique sur les niveaux successifs d'une suite de maillages emboités. Cette méthode permet de réduire considérablement le coût CPU de schéma numérique.